4369. Arson
There is a common
web in front of you. However, as an experienced contester, you noticed that it
is a connected graph with n vertices and m edges. If you fire some vertex, it
will light up, after a second all adjacent vertices light up, then all adjacent
ones with already burning will light up, etc.
You know which
vertices will be fired in the web (all at the same time). Find how many seconds
will pass until the last vertex lights up and find this vertex.
Input. The first line contains integers n (1 ≤ n ≤ 105) and m
(n – 1 ≤ m ≤ 105). Each of the next m lines contains two numbers – the vertex numbers connected with an
edge. The vertices are numbered starting from 1.
The next line contains number k
(1 ≤ k ≤ n) – the number of points to fire. Next
line contains the numbers of k
vertices to be fired.
Output. In the first
line print the time when the last vertex will light up. In the second line
print the number of this vertex. If there are several of them, print the one
with minimum number.
|
Sample
input |
Sample
output |
|
6 6 1 2 2 6 1 5 5 6 3 5 4 5 2 1 2 |
2 3 |
SOLUTION
graphs
- bfs
Algorithm analysis
Breadth First
Search from multiple sources. Push all the fire
points to the queue and start Breadth First Search.
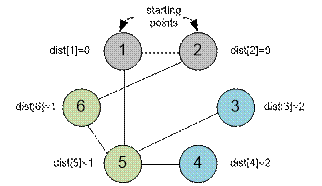
Example
Graph shown in
the sample has the form:
Algorithm realization
Declare arrays for breadth
first search.
vector<int> dist;
vector<vector<int> > g;
queue<int> q;
All sources are already in queue q. Start the breadth first search.
void bfs(void)
{
while (!q.empty())
{
int v = q.front(); q.pop();
for (int to : g[v])
if (dist[to] == -1)
{
q.push(to);
dist[to] = dist[v] + 1;
}
}
}
The main part of the program. Read the input data. Construct the graph.
scanf("%d %d",&n,&m);
g.resize(n+1);
for(i = 0; i < m; i++)
{
scanf("%d
%d",&u,&v);
g[u].push_back(v);
g[v].push_back(u);
}
The dist[i] value
contains the time after which the vertex i will light up.
Initially we set dist[i] = -1.
dist =
vector<int>(n+1,-1);
Read the sources of arson. For each vertex id of arson, set dist[id] = 0 and
push vertex id to the queue.
scanf("%d",&k);
for(i = 0; i < k; i++)
{
scanf("%d",&id);
dist[id] = 0;
q.push(id);
}
Run breadth first search.
bfs();
We are looking for the vertex id, that will light up the last. The mx variable contains the time after
which the id vertex will light up.
mx = -1;
for(i = 1; i <= n; i++)
if (dist[i]
> mx)
{
mx = dist[i];
id = i;
}
Print the time dist[id], after
which the last vertex id will light up. Next, print the id number of this vertex.
printf("%d\n",dist[id]);
printf("%d\n",id);
Java realization
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g;
static Queue<Integer> q = new LinkedList<Integer>();
static int dist[];
static int n, m;
static void bfs()
{
while(!q.isEmpty())
{
int v = q.poll();
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (dist[to] == -1)
{
q.add(to);
dist[to] = dist[v] + 1;
}
}
}
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt(); m = con.nextInt();
g = new ArrayList[n+1];
for(int i = 0; i <= n; i++)
g[i] = new ArrayList<Integer>();
dist = new int[n+1];
for (int i = 0; i < m; i++)
{
int u = con.nextInt();
int v = con.nextInt();
g[u].add(v);
g[v].add(u);
}
Arrays.fill(dist,-1);
int k = con.nextInt();
for (int i = 0; i < k; i++)
{
int id = con.nextInt();
dist[id] = 0;
q.add(id);
}
bfs();
int max = -1, id = -1;
for(int i = 1; i <= n; i++)
if (dist[i] > max)
{
max = dist[i];
id = i;
}
System.out.println(dist[id]);
System.out.println(id);
con.close();
}
}